Spell Test PLAY Match Gravity Commutative Property of Addition Click card to see definition 👆 Tap card to see definition 👆 x y= y xIf x x x and y y y are real numbers such that x y = 7 xy=7 x y = 7 and x 3 y 3 = 133 x^3y^3=133 x 3 y 3 = 1 3 3, find the value of x y xy x y Submit your answer 3 3 ( 1640 ) 1 3 \sqrt{\sqrt{\sqrt3{\color{#3D99F6}{}} {\sqrt3{\color{#3D99F6}{} \color{teal}{3(1640) 1}}}}} 3 6 4 0 0 0 3 6 4 0 0 0 3 ( 1 6 4 0 ) 1Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and y In the activity method, the identities are verified by cutting and pasting paper

Solved Prove The Identity Simplify At Each Step 3 Cos X Chegg Com
(x+y)^3 identity class 9
(x+y)^3 identity class 9-X = 2 y = 2 # and print (x > 0 and y < 0) # True # or print (x > 0 or y < 0) # True # not print (not (x > 0 and y < 0)) # False Identity Operators Identity operators are used to check if two objects point to the same object, with the same memory location Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Who are the experts?X y x' x'y xx'y xy 0 0 1 0 0 0 0 1 1 1 1 1 1 0 0 0 Stack Exchange Network Stack Exchange network consists of 179 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersExample 3 Jeremy uses the polynomial identity (x² – y?)² (2xy)² = (x² y²)² to generate the Pythagorean Triple, 9, 40, 41 What values of x and y did he use to generate the values for the three sides of a right triangle?
Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms x^ {3}y^ {3}=x^ {3}y^ {3} x 3 y 3 = x 3 y 3 Subtract x^ {3} from both sides Subtract x 3 from both sides x^ {3}y^ {3}x^ {3}=y^ {3} x 3 y 3 − x 3 = y 3 Combine x^ {3} and x^ {3} to get 0Algebra Formulas for Class 9 Algebra is a branch of mathematics in which universal symbols and letters are used to represent quantities and numbers in equations and formulas Algebra is divided into two sections elementary algebra and modern algebra (Abstract algebra) Algebra formulas for Class 9 comprise formulas relating to algebra identities or expressions
Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2Prove the identity 3 cos (x y) 3 cos (x y) = 6 cos (x) cos (y) Use a Reciprocal Identity, and then rewrite as a single rational expression 7 tan (x) 7 tan (y) = 7 sin (y) cos (y) cos (x) = cos (x) cos (y) Use an Addition or Subtraction Formula to simplify Prove the identity sin ( 1The two polynomials are called as special binomials because the first term in each expression is same Hence, the product of them is called as the special product of binomials It is written in the following mathematical form algebraically ( x − a) ( x − b) The product of them is equal to an algebraic expression x 2 − ( a b) x a b




Adidas X Y 3 Shiku Run Black Creme Fx1416 Garmentory




Expand Each Of The Following Using Suitable Identities 2x 5y 3z 2
This identity can also be expressed as, This is the required standard algebraic identity In the expression, if we replace ywith (−y), we will get the identity x3−y3 Now, let's further verify this numerically with an example To verify, let's take the values for xand yand put inTherefore, x=50, and y=3 I do not get thisAnswer 1 There are two words that start with a, two that start with b, two that start with c, for a total of \(222\text{}\) Answer 2 There are three choices for the first letter and two choices for the second letter, for a total of \(3 \cdot 2\text{}\) Since the two answers are both answers to
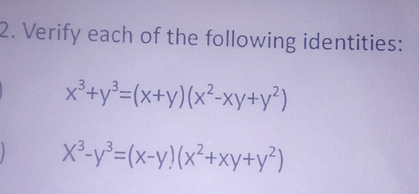



2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr




Expand Each Of The Following Using Suitable Identities
It is read as $x$ plus $y$ whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ${(xy)}^3$ $\,=\,$ $x^3y^33x^2y3xy^2$ Proofs The cube of $x$ plus $y$ identity can be proved in two different mathematical approaches Algebraic method Learn how to derive the expansion of cube of $x$ plus $y$ identity by the For $x,y$ in G, prove that $x = y =e$ if $xy^2=y^3x $ and $yx^2=x^3y$ where $e$ is the identity element in G I have filled pages trying to solve but unable to reach Find the value of 53^3 using the identity (xy)^3=x^33x^2y3xy^2y^2 Hint 53^3 =(503)^3;



Identity Mathematics Wikipedia




Rational Functions And Endomorphisms Separable Endomorphisms Parallelogram Identity And Degree Map
Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have, So we have, (x 3 8y 3 27z 3 – 18xyz) = (x) 3 (2y) 3 (3z) 3 – 3(x)(2y)(3z)= (x 2y 3z)(x 2 4y 2 9z 2 – 2xy – 6yz – 3zx)(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x^2y 3xy^2 3 ( x^2 y^2 2xy ) z 3x z^2 3yz^2 =x^3y^3z^3 3x^2 y3xy^2 3x^2 z 3y^2 z 6xyz 3xz^2 3 yz^2 arrange in orderTherefore, x = 50 and y = 3 I dont get this at all?




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube



1
We can find the value by using the trigonometric identity of sin 3 x Answer The formula of Sin 3 x is (3 sinx sin3x)/4 Let's proceed step by step Explanation As per trigonometric identity, we have sin 3x = 3sin x 4sin 3 x On transposing terms, 4 sin 3 x = 3sinx sin 3x Divide both sides of the equation 4 sin 3 x = 3sinx sin 3x by The formula is (xy)³=x³3x²y3xy²y³ You convert it to (xy)³=x³3xy(xy)y³ for an illustration You take the drawing of the formula (xy)³=x³3x²y3xy²y³ from above and replace a by the difference xyExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text Prove the identity 3 cos (x y) 3 cos (x y) = 6 cos (x) cos (y)




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



A Minus B Whole Cube Formula Examples A B 3 Formula
Solution THEOREM 3 (a) Law of Absorption yxx = x yxx = yxx1 by identity (Ax 2b) = x (y1) by distributivity (Ax 4a) = x1 by Theorem 2 (a) = x by identity (Ax 2b) THEOREM 3 (b) x (xy) = x by duality THEOREM 6 (a) De Morgan's Laws (xy)' = x'y' Proof We will prove that x'y' is a complement of xy by proving that x'y' satisfies Find the value of 533 using the identity (x y)3 = x3 3x2y 3xy2 y3 Hint 533 = (50 3)3; Use the identity (xy)(x2−xyy2)=x3y3 to find the sum of two numbers if the product of the numbers is 10, the sum of the squares of the numbers is 29, and the sum of the cubes of the numbers is 133 Enter your answer as a number, like this 42




Find The Following Squares By Using The Identities I B 7 2




Solved Prove The Identity Simplify At Each Step 3 Cos X Chegg Com
In the LHS of the identity,we put x=2&y=3 Similarly in the RHS of the identity,we put x=2&y=3 Thus, the identity is verified Now, let's expand the second Identity If we replace ywith (−y)the expression changes to (x−y)3 So to find the expansion of (x−y)3, we can replace ywith (−y)in (xy)3=x23x2y3xy2y3 It seems more like this should be an inequality (xy)^3 (yz)3 (zx)^3 >= 3 (xy) (yz) (zx) But that is not the question set Please note that this is the first chapter and all that has been covered is basic number theory, rational powers, inequalities and divisibilityFactorization of x 3 y 3 It can be seen in most book that x 3 y 3 can be factorized by dividing the expression by (x y) After division we get a quotient of (x 2 xy y 2) with no remainder Therefore However, this method involves knowing the factor (x y) beforehand (and the understanding of Factor Theorem)




Solved By Inspecting The Form Of The Thermodynamic Identity Du Tds Pdv And The Definition Of The Differential Df X Y 3 Dx 3 Dy Select The Correct Expression That Completes The Following




Let G X E R X 1 Be The Set Of All Real Numbers Greater Than 1 For X Y E G Define X Y Xy X Y 2 1 Show That The Operation Is
In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B (which might contain some variables) produce the same value for all values of the variables within a certain range of validity In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between Click here 👆 to get an answer to your question ️ solve using identity (x2/3y)^3 thessoul thessoul Math Secondary School answered Solve using identity (x2/3y)^3 2 See answers Advertisement Advertisement HarishAS HarishAS Hey friend, Harish here Here isFactor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5
Problem Solve (x 3) (x – 3) using algebraic identities Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5)X^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra Student Email obuong3@aolcom




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Chapter 2 Polynomials Ncert Solutions Class 9 Maths
Use the identity (xy)(x−y)=x2−y2 to find the difference of two numbers if the sum of the numbers is 12 and the difference of the squares of the numbers is 48 Enter your answer as a number, like this 42SolutionShow Solution It is known that, a 3 − b 3 = ( a − b) ( a 2 b 2 a b) ( x y) 3 − ( x − y) 3 = { ( x y) − ( x − y) } { ( x y) 2 ( x − y) 2 ( x y) ( x − y) } = 2 y ( x 2 y 2 2 x y x 2 y 2 − 2 x y x 2 − y 2) = 2 y ( 3 x 2 y 2) Concept Factorisation using Identity a3 b3 = (a b) (a2 ab b2) Report ErrorProof Question How many 2letter words start with a, b, or c and end with either y or z?



Which Is A Polynomial Identity A X3 Y3 X Yx2 Xy Y Gauthmath




Values Mm Of X Y And Z Coordinates Of Landmark Locations Identity Download Table
There are many methods that one can use to prove an identity The simplest is to use algebraic manipulation, as we have demonstrated in the previous examples In an algebraic proof, there are three acceptable approaches To prove that \x^3y^3 = (xy) (x^2xyy^2),\ we start from the righthand side, because it is more complicated than Show that $$(xy)^3(yz)^3(zx)^3 = 3(xy)(yz)(zx)$$ This can be shown through expansion but there is a more elegant solution I cannot discover anything I would consider elegant Can anyone hConsider x^ {2}y^ {2}xy22xy as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factor




If X Y Z 0 Show That X 3 Y 3



2
For the Transformation T, write the T^ 1 T ( x , y ) ( x , y ) T^ 1 ( x , y ) ( x , y ) The Rotation R maps all 60° about O the center of the regular hexagon State the image of B for the following rotation R^1 = A The Rotation R maps all 60° about O the center of the regular hexagonElaborating x 3 y 3 using identity a 3 b 3 = (a b)(a 2 ab b 2) = x ( x y)(x 2 xy y 2) 3xy (x y ) Taking common x( x y ) in both the terms = x ( x y){x 2 xy y 2 3y} ∴ x (x 3 y 3) 3xy ( x y) = x ( x y )(x 2 xy y 2 3y)Examples on (a b)^3 Formula Example 1 Solve the following expression using (a b) 3 formula (2x 3y) 3 Solution To find (2x 3y) 3 Using (a b) 3 Formula, (a b) 3 = a 3 3a 2 b 3ab 2 b 3 = (2x) 3 3 × (2x) 2 × 3y 3 × (2x) × (3y) 2 (3y) 3 = 8x 3 36x 2 y 54xy 2 27y 3 Answer (2x 3y) 3 = 8x 3 36x 2 y 54xy 2 27y 3 Example 2 Find the value of x 3 y 3 if




Solved Arrange The Steps In The Correct Order To Prove The Chegg Com




Algebraic Identities Of Polynomials A Plus Topper
Verify the Identity x^3y^3=(xy)(x^2xyy^2) Simplify the right side Tap for more steps Simplify Tap for more steps Expand by multiplying each term in the first expression by each term in the second expression Simplify terms Tap for more steps Simplify each termThis problem has been solved!




Product Sum And Sum Product Identities Lecture Notes Math 1 Docsity




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Algebraic Identities Of Polynomials A Plus Topper




6 Problems On System Of The Equations Midterm Exam Math 2270 Docsity
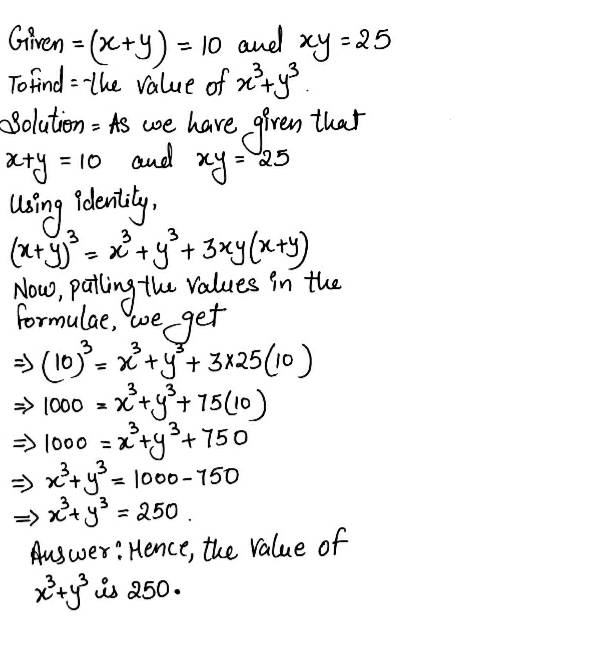



Example 2 62 If X Y 10 And Xy 25 Find The Value Of X 3 Y 3 Snapsolve



If X 3 And Y 1 Find The Values Of Each Of The Following Using In Identity I 9y 2 4x 2 81y 4 36x 2y 2 16x 4 Sarthaks Econnect Largest Online Education Community




Polynomials Ppt Video Online Download




Polynomial Identity From Wolfram Mathworld




Solved 2x Y 52 8 3 2y 2 10 41 Y 42 23 3c Y 1 1 I Y 7 21 3y




X3 Y3 Class 9 Maths Algebra Identity Derivation Youtube




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




Rd Sharma Solutions Class 9 Chapter 4 Algebraic Identities Updated For 21 22




Pdf Units In Quasigroups With Classical Bol Moufang Type Identities



Identity Vs Equation Acute Angel
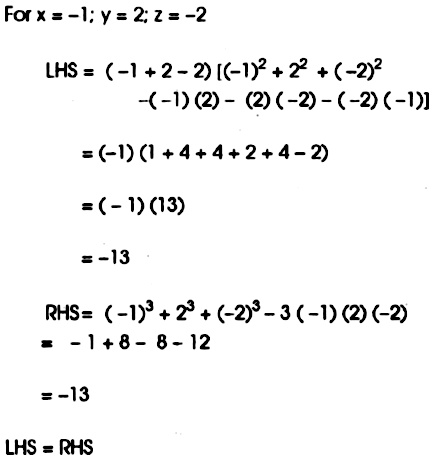



Verify The Identity X Y Z X 2 Y 2 Z 2 Xy Yz Zx X 3 Y 3 Z 3 3xyzwhen X 1 Y 2 Z 2 Snapsolve



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




Experiment No 2 Boolean Algebra




Verify The Following Identity X Y 3 X3 Y3 3xy X Y Brainly In




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




X Y 3 2 X Y 3 2 Solve By Using Suitable Identity Brainly In
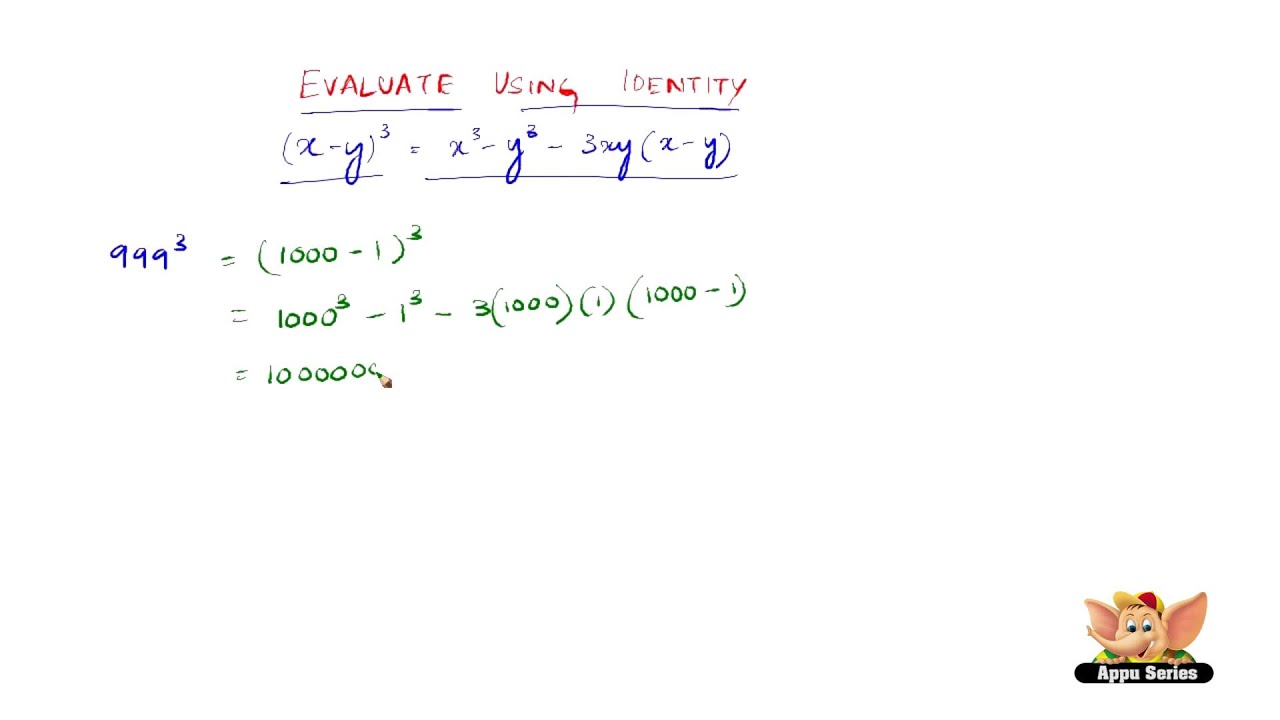



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Polynomials Ppt Video Online Download




Solved Prove The Identity 3 Tan X 3 Tan Cos X Cos Y 3 Chegg Com




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




If X Y Z 0 Then Find The Value Of X 3 Y 3 Z 3 Maths Algebraic Expressions And Identities Meritnation Com




Pdf On Representation Of An Integer As A Sum By X 2 Y 2 Z 2 And The Modular Equations Of Degree 3 And 5 Alexander Berkovich Academia Edu




Polynomials Ppt Video Online Download




If X Y 26 And Xy 3 Find The Value Of X Y 4y 2 A A 4yi If 26 And 3 Maths Algebraic Expressions And Identities Meritnation Com




Formula
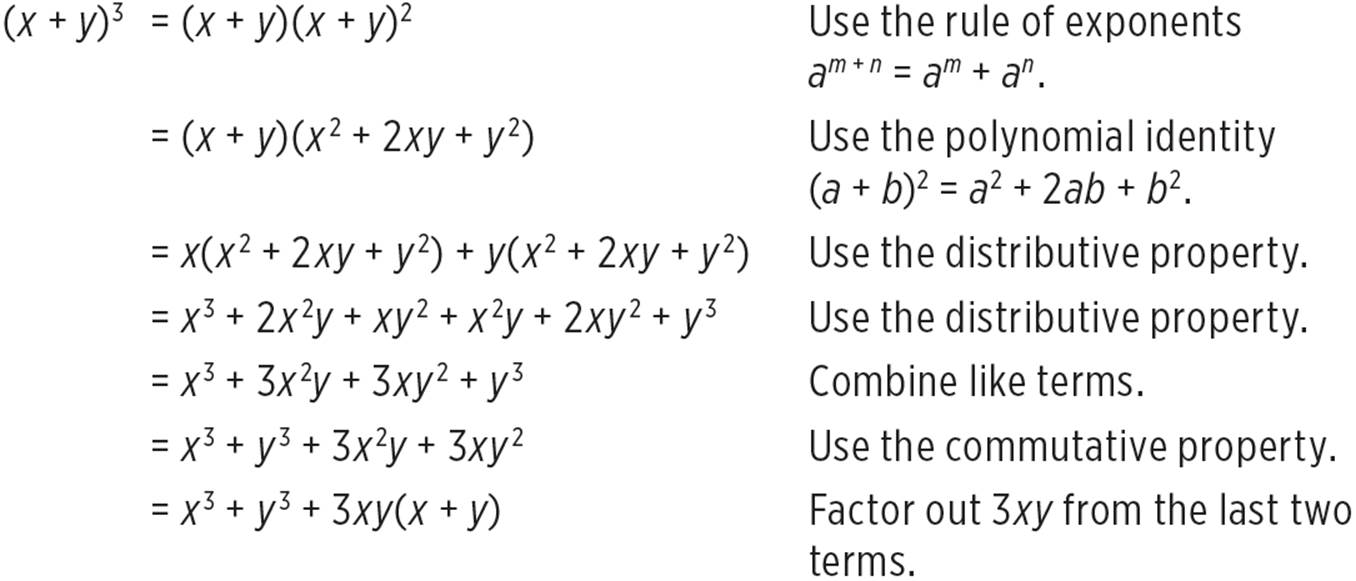



Polynomial Identities Complex Numbers And Polynomials High School Algebra Ii Unlocked 16




Algebraic Identities Standard Algebraic Identities With Examples




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




X 2 3 Y Expand It Using Suitable Identities Brainly In




Answered Prove The Identity Sin X Y Sin X Bartleby



1
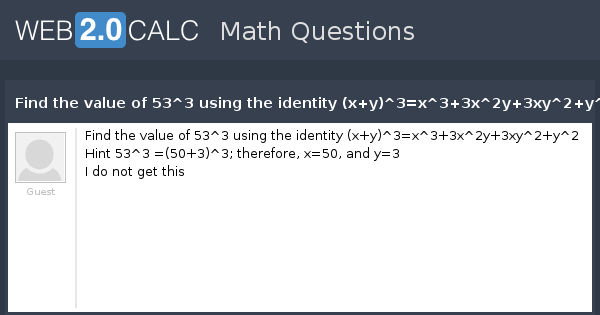



View Question Find The Value Of 53 3 Using The Identity X Y 3 X 3 3x 2y 3xy 2 Y 2




Algebraic Identities Worksheet




Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Verify That X 3 Y 3 Z 3 3xyz 1




An Operation Is Defined On Set Of Real Number By X Y X Y 2xy If The Identity Is Myschool




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Using The Identity X A X B X 2 A B X Ab Find Out The Followingproducts Xy 3 Xy 2 Snapsolve
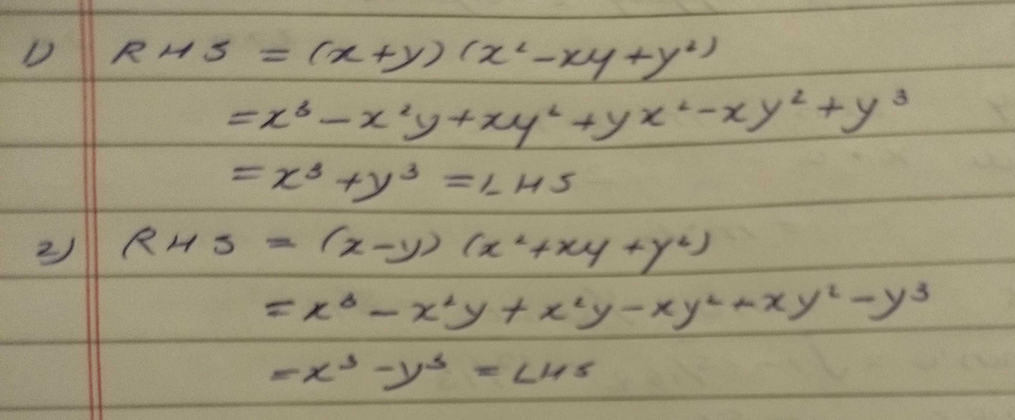



2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr




Lines And Am Nles




Verify




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Chegg Com



1




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Identity Identity Square Of X Y Z Geogebra




Cbse Class 9 Basic Concept Of Algebraic Identity Part 1 In Hindi Offered By Unacademy




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 4 Y 3 X 2 16 X Y 12 Y 2 9
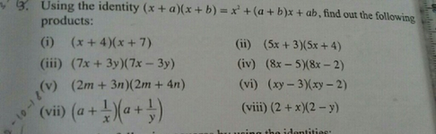



V3 Using The Identity X A X B X A B X Ab Find Ou Scholr




Ex 9 5 3 Find The Squares Xy 3z 2 Using The Algebra Identities



Simplify Each Of The Following Expressions I X Y Z 2 X Y 2 Z 3 2 X 2 Y 3 Z 4 2 Ii X Y 2z 2 X 2 Y 2 3z 2 4xy Sarthaks Econnect Largest Online Education Community




What Is An Identity Shashank Tutorial




Example 11 Using Identity I Find 2x 3y 2 Algebra Class 8




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Art Of Problem Solving



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




Algebra Precalculus Name For The Identity X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Xz Zy Mathematics Stack Exchange




Exam 3 Homework Set Week 11 Flashcards Quizlet



Find The Value Of X3 Y3 12xy 64 When X Y 4 Maths 9th Pyranic




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044



2



Rd Sharma Solutions Class 9 Chapter 4 Algebraic Identities




Polynomials Exercise 2 5 Pocket Gyan



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Cbse Class 9 Algebraic Identities Offered By Unacademy




Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Cos X Chegg Com




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




2 Y 3 Y 4 Cheap Sale 56 Off Www Nogracias Org




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



X Y 2




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



0 件のコメント:
コメントを投稿