30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir (BC) = 30 cm (AB) = 25 cm (AC) = 5 cm olmak zorundadır 15 75 90 üçgeni özel kuralları yukarıda verildiği şekildedir Açılarını bilinmesiyle çok rahat uzunlukları da bilinmektedir Açıları ve uzunluk ölçüleri bilinen üçgenlerin alan hesaplama işlemi de oldukça basittir Yani bilinen 15 75 90 üçgeni kuralı ile o özel üçgenle ilgili açı, uzunluk, yükseklik ve 30 60 90 üçgeni 30 60 90 üçgeni çoğu soruda karşımıza gelir o nedenle bu üçgenin özelliklerini iyi bilmek gerekir Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalı Önce bu 90 derecelik açıyı bulun bu açının karşısındaki kenara hipotenüs adı verilir ve bu kenar dik üçgenin en uzun

Zoqr8sxmfxasqm
30 60 90 üçgeninin özellikleri
30 60 90 üçgeninin özellikleri- 30 60 90 üçgeni kenarlarıBF, FG ve GB BFG üçgeninin kenarları olduğundan BF = FG = GB Sevgiler üçgenine yabancı biri için bu üçgen anlamsızdır ama tek bir çizgiyle biri ikizkenar diğeri bir üçgeni olan iki anlamlı üçgen elde ediverir Mühim olan az önceki soruda 45 ve 15 açılarında olduğu gibi bu açıları birbirinden30 – 60 – 90 ÜÇGENİ Eşkenar üçgende15 75 90 üçgeni ispatı 75 90 üçgeninin özelliği Iç açılarından bir tanesinin açı derecesi 90 olan üçgenlerdir Çemberde ise çapı tam göre açı ölçüsü 90 derece olurPisagor TeoremiPisagor teoremi;Üçgeni (2√3) İSPAT Dik üçgen 15 75 90 üçgeni işlemli em iyi secicem gereksiz Dik Üçgende Trigonometri Bikifi Finding the area of a $$ triangle with the
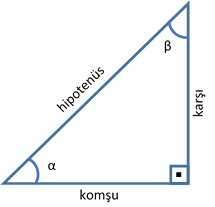



Dik Ucgende Trigonometrik Hesaplamalar
4 24 x 6 cm bu 4 luruz 53最も人気のある! 75 15 üçgeninin özelliği 15 üçgeni özelliği 新しい 小学 5 年生 算数 割合 文章 問題 小学5年生の算数 百分率と歩合割合の表し方 練習問題プリント 教材の新学習指導要領への対応について ただいまちびむすドリル小学生では公開中の教材の 新学習指導要領年度スタートへ" üçgeni" burada yönlendirir Çizim aracı için bkz set kare İkizkenar üçgenlerin en az iki eşit kenara sahip olduğu, yani eşkenar üçgenlerin ikizkenar olduğu tanımını kullanarak, üçgen türlerinin Euler diyagramındaki bazı özel üçgenlerin konumu Bir özel dik üçgen bir olan dik üçgen üzerinde hesaplamalar yapar bazı düzenli özelliği ile
Bu üçgenlerin alanları birbirine eşit olduğuna göre ABC üçgeninin IBCI kenarına ait yüksekliğinin uzunluğu kaç santimetredir?50 60 70 80 90 100 110 1 130 140 150 030 3060 60 90 1 150 50 0 30 1 150 60 70 80 90 100 110 1 130 140 150 50 0 30 1 150 60 70 80 90 100 110 1 130 140 150 Ölçüm Hatası (˚m) Mesafe (mm) Ölçüm Hatası (˚m) Mesafe (mm) Ölçüm Hatası (˚m) Mesafe15 75 90 Üçgeni kuralı geometri dersinde özel üçgenler konusu adında yer alır Diğer özel üçgenler kadar yoğun bir şekilde soru öbekleri bulAD//BE//CFTüm üçgenlerde iç açıların ölçülerinin toplamı180° dir Üçgenlerin ikişer açılarının ölçülerieşit ise üçüncü açı ölçüleri de eşit olur O hâldebu özellik ikişer açı ölçüsü kullanarak açıaçıbenzerlik özelliği olarak da söylenebilir 35 39 SORULAR 36 40 37 41 13 14 15 37 53 90 üçgeni şükela tümü bugün matematikçilerin sin 37'nin ve
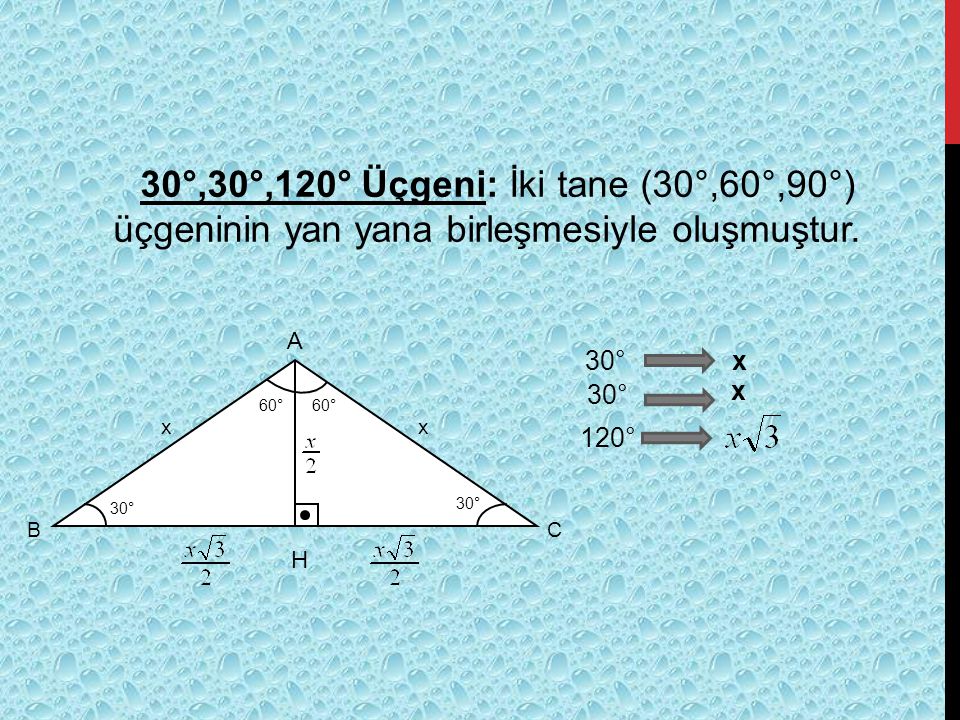
30 30 1 üçgeni 30 30 1 üçgeni bir ikizkenar üçgendir 1 derecelik açının karşısından karşı kenara dikme indirdiğinizde iki tane eş 30 60 90 üçgeni elde ederiz Yamuk sorularında Yamuk sorularında dikme indirdiğimiz zaman 30 60 90 üçgeni karşımıza çok çıkmaktadırYine aynı oranlarla kenarları bulmak ve alan hesaplamak kolay olacaktır 45 45 90 üçgeni de işimizi kolaylaştıracak özel üçgenlerden biridir 45 45 90 üçgenini iyi öğrenirsek temel bazı trigonometrik bağıntıları da öğrenmiş oluruz Bu nedenle bu üçgeni ve özelliklerini bilmek önemlidir Öncelikle en az bu üçgen kadar önemli 30 60 90 üçgeni olduğunu belirtelim Bu özel üçgenleüçgeninin birçok farklı özelliği ön plana çıkmaktadır – İki dar açının toplamı diğer iç açının toplamına eşittir 15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Yani dikme ile hipotenüs arasında h 4h




Mr Pen Architectural Ucgen Cetvel Seti 30 5 Cm Ucgen Olcek 11 Inc 30 60 Ve 8 Inc 45 90 Ucgen Amazon Com Tr Ofis Ve Kirtasiye




15 75 90 Ucgeni Not Bu
(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz DİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 55 Kişisel Gelişim Geometri Psikoloji Harfler Science Eğitim Banyo Daha fazla bilgi Kullanıcılar bu fikirlere de bayılıyorRead özel üçgenler (15°75 30 30 1 üçgeni sorularda ve sınavlarda öğrencilerin sıkça karşısına çıkmaktadır Soruları yapabilmek açısından bu üçgenin özelliklerini bilmek gereklidir 30 30 1 üçgeni bir özel ikizkenar üçgendir İkizkenar üçgen taban açıları aynı olan üçgendir ve açıların gördüğü kenar uzunlukları birbirine eşittir 30 30 1 üçgeninin bir diğer özelliği √ 15 75 90 üçgeni kuralı 75 90 üçgenin kuralı Daha iyisi yapılana kadar en iyisi bu75 15 90 üçgeni özelliği;Mm lens sample photos;




Special Right Triangles Examples Worked Solutions Videos Special Right Triangle Right Triangle Triangle Worksheet




Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com
Bu nedenle bu üçgeni öğrenmeden önce eğer bilmiyorsanız 30 60 90 üçgeni ile 45 45 90 üçgeni hakkında bilgi sahibi olmanız tavsiye edilmektedir 15 75 90 Üçgeninde Dikme Özelliği 15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com 15 75 90 üçgenin kuralı 15 75 90 üçgenin kuralıEski sevgiliyi unutmak 3;4 24 x 6 cm bu 4 luruz 53 The 27 63 90 Triangle Robertlovespi NetBir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m(A) = 90° BC kenarı hipotenüsAB ve AC kenarlarıdik kenarlardır 15 75 90 Üçgeni Özellikleri




30 30 1 Ucgeni Not Bu




Net Fikir
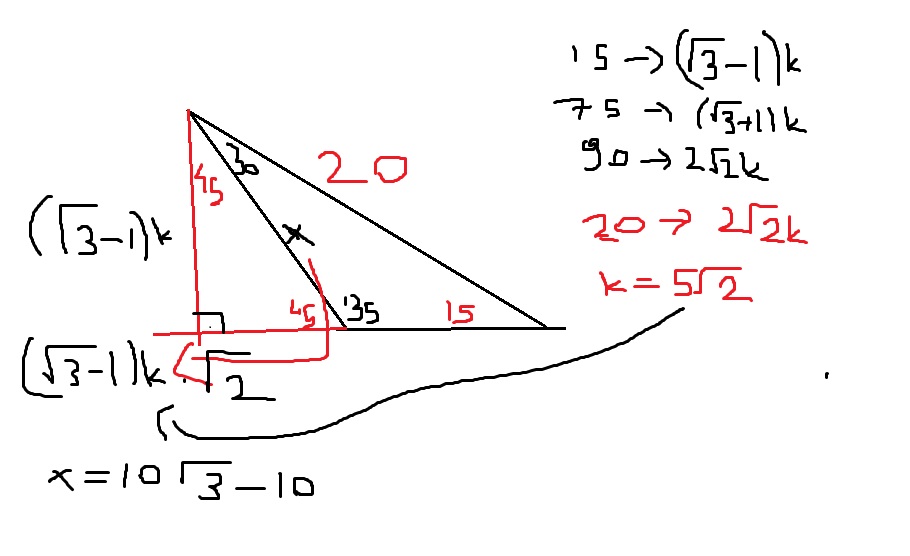
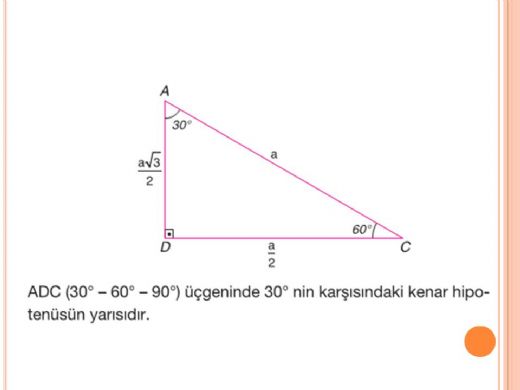
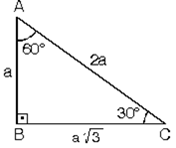
(30° 60° 90°) dik üçgeninde; 15 ve 60 olarak böldüğünüzde ise karşınıza bir 30 60 90 üçgeni ve de diğer tarafta kalan açıları 15 15 150 olan bir ikizkenar üçgen çıkacaktır bu durumda şöyle bir sonuç çıkar karşımıza 15 derecenin karşısındaki kenara a değerini verirsek, 75 derecenin karşısındaki kenar da 2aakök3 olacaktır 90'nın karşını da pisagor teoreminden hesaplayın, işinizDik Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir
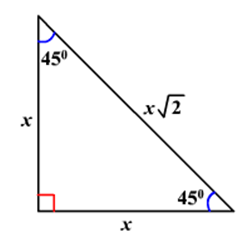



Dik Ucgende Trigonometrik Oranlar
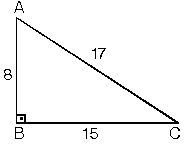



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
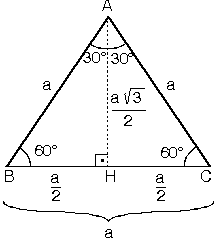
リコーダー運指表 全音楽譜出版社 ドレミファソラシドだけで演奏できる曲の楽譜 全音楽譜出版社 小学生のための歌とソプラノ リコーダーで奏でる すぐ使える無料楽譜 スタジオジブリ 天空の城ラピュタ 全4曲 ピアノ塾 山のポルカ 小学生の音楽3 より15 75 90 ÜçgeniPediatric Associates30 60 90 üçgeni Fotoğraflar, videolar ve diğer malzemeler New photos are added daily from a wide variety of categories including abstract, fashion, nature, technology and much more 30°60°90° Triangle – Explanation & Examples 30 60 90 Triangle Definition Learn About The Triangle Caddell Prep Online Exploring cosine in a 30,60,90 triangleüçgeni ve ispatı Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır 30°'nin karşısındaki kenarın katıdır İspatı ise eşkenar üçgen vasıtasıyla yapılır Kenarları 2 cm olan bir eşkenar üçgende köşeden indirilen dikme kenarı iki eş




A Ladder 15m Long Just Reaches The Top Of A Vertical Wall If The Ladder Makes An Angle Of 60 With The Brainly In
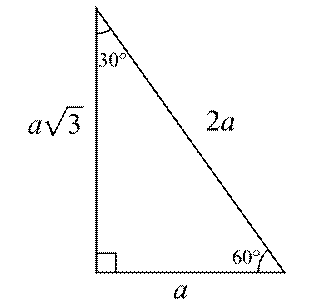



En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari Sorulari
30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir Yani dikme ile hipotenüs arasında h 4h bağıntısı vardır 15 75 90 üçgeninde dikme özelliği Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz 30 60 90 üçgeni 15 75 90 üçgeni özelliği bu makaledeki notlar En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmas şekilde m 90 kenarı hipotenüs ve 15 75 90 Üçgeni Kuralları 15 75 90 üçgeni0以上 15 75 90 üçgeni özelliği 75 90 özel üçgeni özellikleri 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in
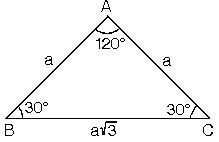



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Pow Bylge
印刷可能 15 75 90 üçgeninin özelliği 75 90 üçgeni özellikleri General description The Census collected individual records on all children receiving care and support, including those looked after by a local authority, who had an open case with a local authority on the 31 March that had been open for the three months from 1 January to 31 MarchAngle Sums and the Right15 75 90 üçgeni alan formülü 15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olarİç açıları 15 derece ve 75 derece ile 90 derece oluşan özel üçgene üçgeni denmektedir Bu üçgen aynı zamanda iç açıları kapsamındaRead özel üçgenler (30°60°90° üçgeni) from the story Matematik Formülleri by TheMuhammedALI with 2,101 reads wattys15, formüller, geometri Resime bakın




Hatas Teknik Resim Gonyesi Acryl Akrilik 32 Cm 30 60 90 Fiyatlari Ve Ozellikleri




Mr Pen Architectural Ucgen Cetvel Seti 30 5 Cm Ucgen Olcek 11 Inc 30 60 Ve 8 Inc 45 90 Ucgen Amazon Com Tr Ofis Ve Kirtasiye
A) 6 B) 7 C) 8 D) 10 E) 12 wwwmatematikkolaynet Çözüm BCD üçgeni bir 30 60 90 üçgenidir 30 nin karşısı 12 ise 90 nin karşısı bunun iki katı yani 24 cm dir ABC üçgeni bir üçgenidir Bu üçgenin 1 yüksekliği, tabanın 'ü dür Bu sebeple;Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 75 90 üçgeninin en önemliÜçgeni İKİZKENAR ÜÇGEN İkizkenar üçgende tepe açısından inen;90 15 75 Ucgeninin Ozelligi Kurulustan konuya iliskin yapilan basin aciklamas



15 75 90 Ucgeni Donanimhaber Forum



Dik Ucgen Vikipedi
30 60 90 üçgeni özelliği 30 60 90 üçgeni özelliğiABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir AB = AC = a BH = HC =pisagordan(30° 60° 90°) dik üçgeninde;4 24 x 6 cm bu 4 luruz 53 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine aitA) 6 B) 7 C) 8 D) 10 E) 12 wwwmatematikkolaynet Çözüm BCD üçgeni bir 30 60 90 üçgenidir 30 nin karşısı 12 ise 90 nin karşısı bunun iki katı yani 24 cm dir ABC üçgeni bir üçgenidir Bu üçgenin 1 yüksekliği, tabanın 'ü dür Bu sebeple;Proof Without Words kitabından şahane bir sözsüz kanıtDaha fazlası MY VİDEO EĞİTİM SİTESİ'nde Misafir olarak giriş




Ozel Dik Ucgenler Tekrar Makale Khan Academy




Dik Ucgende Trigonometrik Hesaplamalar
Ikizkenar 15 75 90 Ucgeni Yardim Edebilir Misiniz Cozemedigim 75 15 90 özel üçgeni bu özel üçgende 15 derecelik açının karşısında yer alan kenar uzunluğu 1cm alınırsa 75 derecelik açının karşısındaki kenarın uzunluğu 2 3 cm olur şekildeki gibi iki üçgene ayırırsak 15 15 150 ve 30 60 90 labla ise lbdla3 olacaktır ve15 75 90 ÜÇGENİ VE ÖZELLİKLERİ → 10Sınıf Matematik Dik Üçgen sunusunun 30 30 1 ÜÇGENİ VE ÖZELLİKLERİ slaytını görüntülemektesinizABC üçgeninde m (A) = 90° a 2 =b 2 c 2 ÖZEL DİK ÜÇGENLER 1 (3 4 5) Üçgeni Kenar uzunlukları (3 4 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 8 10), (9 12 15), gibi 2 (5 12 13) Üçgeni Kenarİstanbul'da Hizbullah operasyonu Gri kategoride yer alan üye yakalandı;



Ucgenler Alkan Hoca Matematik Yks Tyt Ays Kpss Ales Dgs Ygs Lys Teog




15 75 90 Ucgeni Webders Net
75 15 90 üçgeni özellikleriÖzel Üçgeni ve Özellikleri 8Sınıf Matematik 22,567,590 Üçgeni ve Özellikleri (Bağıntıları) 8Sınıf Matematik Son Eklenen İçerikler15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur√100以上 75 15 90 üçgeni özelliği 75 90 üçgeni kenar özellikleri A) 6 B) 7 C) 8 D) 10 E) 12 wwwmatematikkolaynet Çözüm BCD üçgeni bir 30 60 90 üçgenidir 30 nin karşısı 12 ise 90 nin karşısı bunun iki katı yani 24 cm dir ABC üçgeni bir üçgenidir Bu üçgenin 1 yüksekliği, tabanın 'ü dür Bu sebeple;X 2 cm buluruz 11 30 60 90 üçgeni dik üçgen Bu özelliği mutlaka öğrenmelisiniz Bu özel üçgenle ilgili sorulan soruların önemli bir kısmı bu orandan gelmektedir Hem dikme oranı hem de kenar oranları iyi bilinirse çok faydalı olacaktır Şunu unutmayalım ki 30 60 90 üçgenine 15 15 150 üçgenini yapıştırırsak 15 75 90 üçgenini elde ederiz




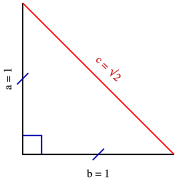
45 45 90 Ucgeni Ikizkenar Dik Ucgen



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir
15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönte 15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönte(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz 15 75 90 üçgeni 2 ayrı çözüm yöntemi15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret e




30 60 90 Ucgeni Ibrahim Hocca




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
30 60 90 Üçgeni 15 75 90 Üçgeni Özelliği Bu makaledeki notlar 15 75 90 üçgeninin özelliği 30 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m = 90° kenarı hipotenüs veYani dikme ile hipotenüs arasında h 4h bağıntısı vardır 15 75 90 üçgeninde dikme özelliği Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz 30 60 90 üçgeni 15 75 90 üçgeni özelliği bu makaledeki notlar En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmas şekilde m 90 kenarı hipotenüs ve Mutlu olmak için gerekenler 11;30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki
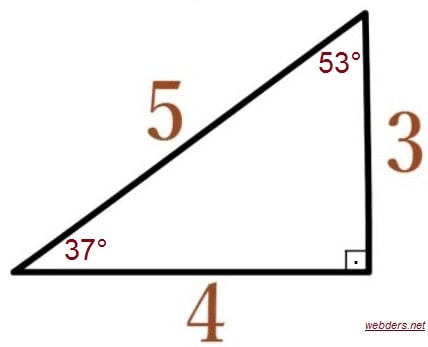



3 4 5 Ucgeni Webders Net




30 60 90 Ucgeni Nedir Ozellikleri Nelerdir Nasil Hesaplanir En Son Haberler Milliyet
1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır İkizkenar Üçgen ÖzellikleriBir açısının derecesi 90° olan üçgen çeşididir Örnek olarak;üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cmKenar uzunlukları veya katları şeklinde olan dik üçgenlerdir Üçgeni Kenar uzunlukları veya katları şeklinde olan dik üçgenlerdir AÇILARINA GÖRE ÖZEL DİK ÜÇGENLER Üçgeni Üçgeni 0 Üçgeni Üçgeni İKİZKENAR ÜÇGEN İkizkenar üçgende tepe açısından inen;
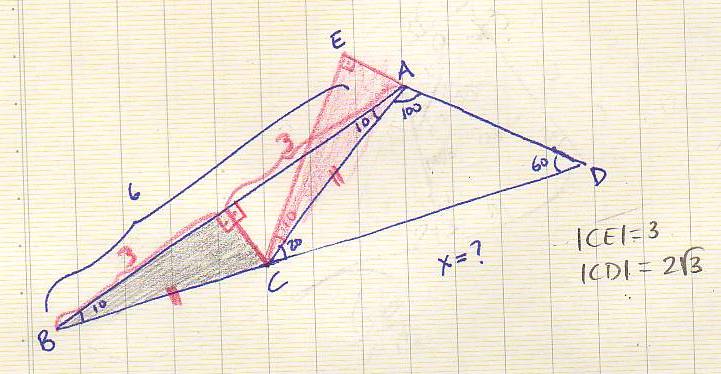



Geometri Sorusu Donanimhaber Forum
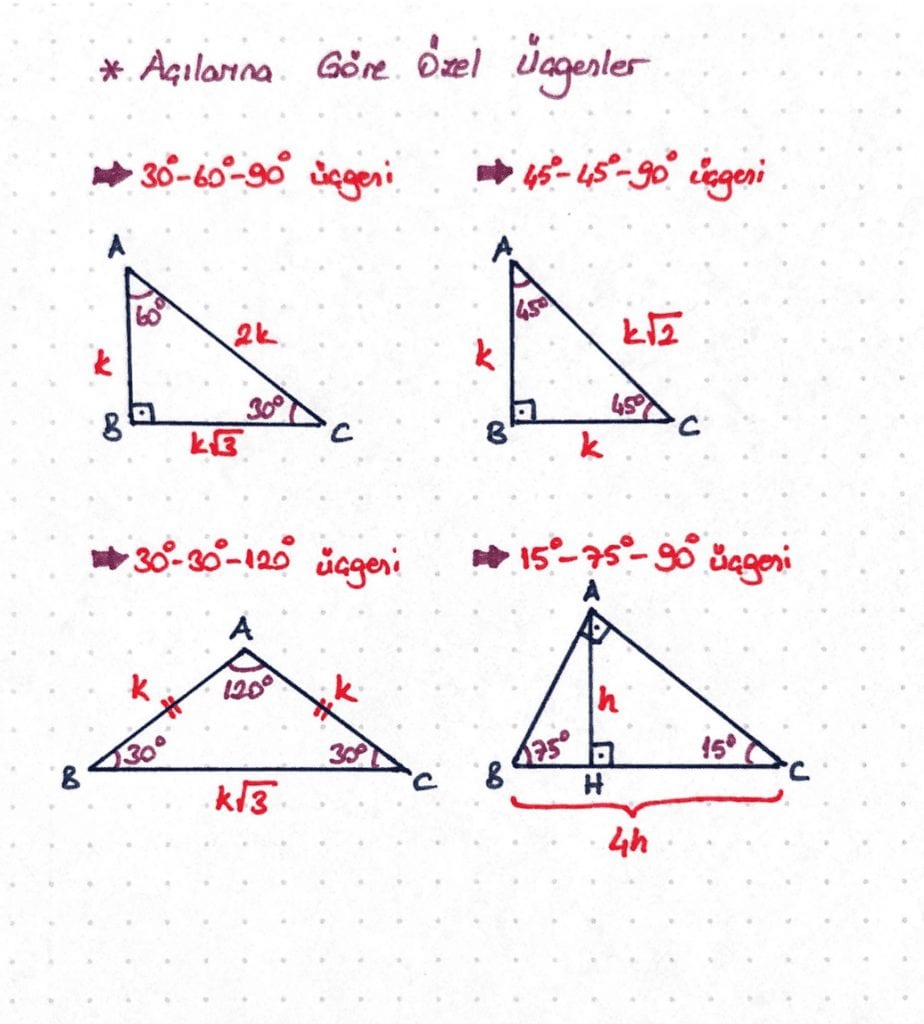



En Hizli 30 60 90 Ucgeni Kurali




Zoqr8sxmfxasqm




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim
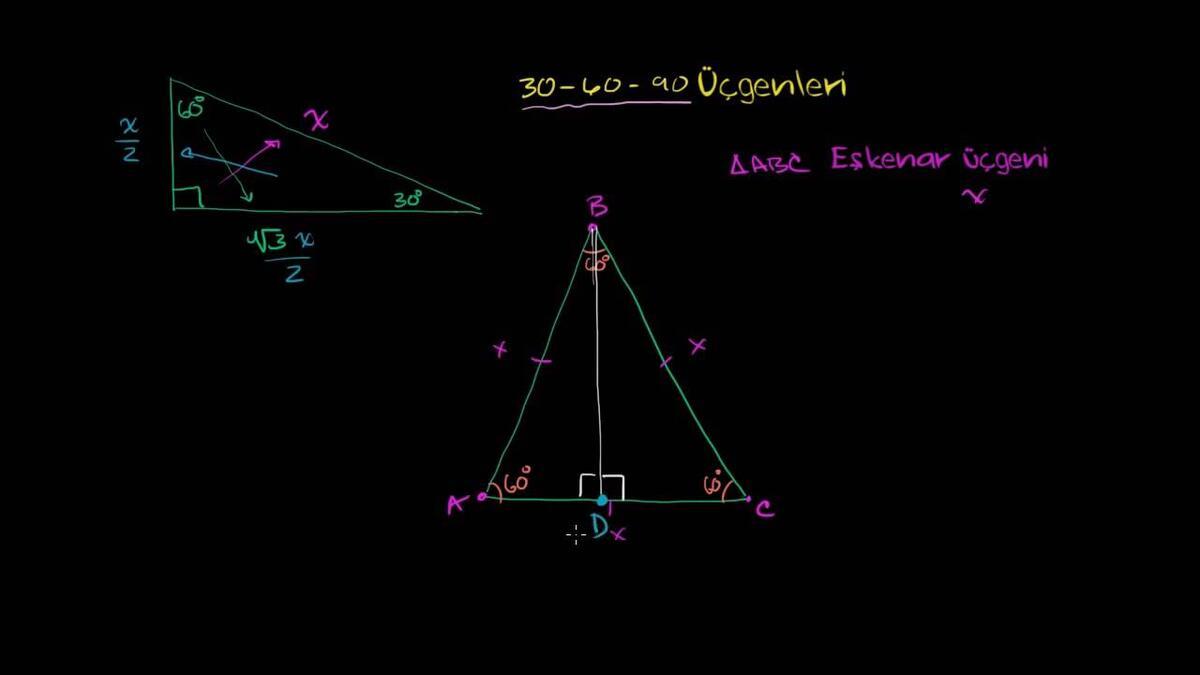



30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri




75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler



45 45 90 Ucgeni Matematikce




90 60 30 Ucgeni




22 5 67 5 90 Ucgeni Konu Anlatimi Ve Ozellikleri Eodev Com




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik
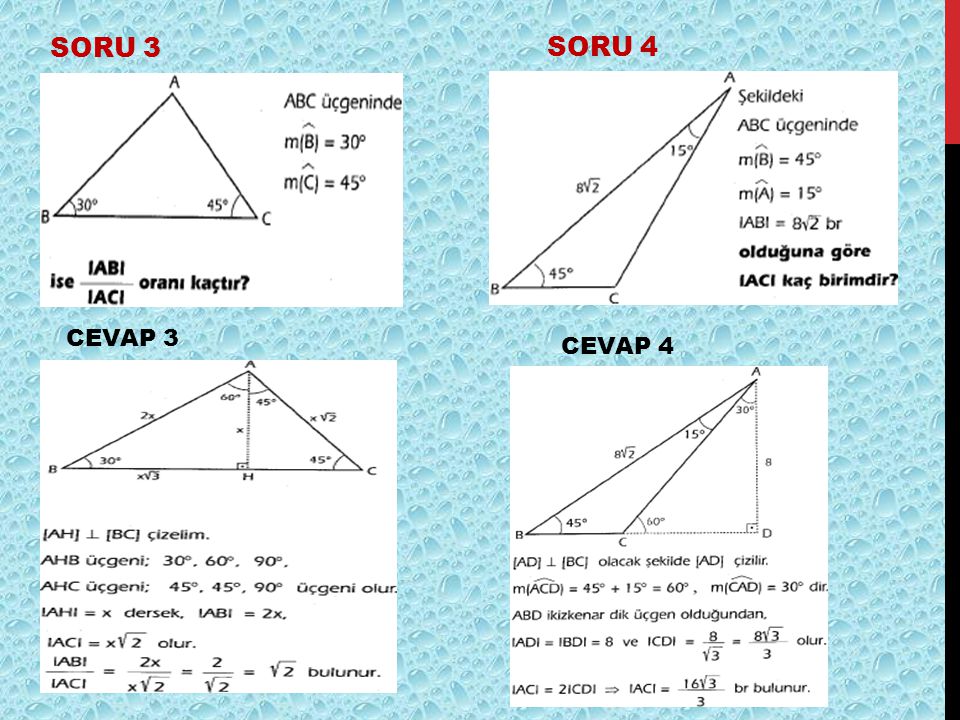



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Hatas Teknik Okul Ogrenci Gonye Seti 26 Cm 30 60 90 Ve 45 45 90 Fiyatlari Ve Ozellikleri




Trigonometri 30 60 90 Ve 45 45 90 Ucgenleri Ile Trigonometrik Oranlari Youtube




Eskenar Ucgen Alani Not Bu




15 75 90 Ucgeni Ozellikleri Ve Kurallari
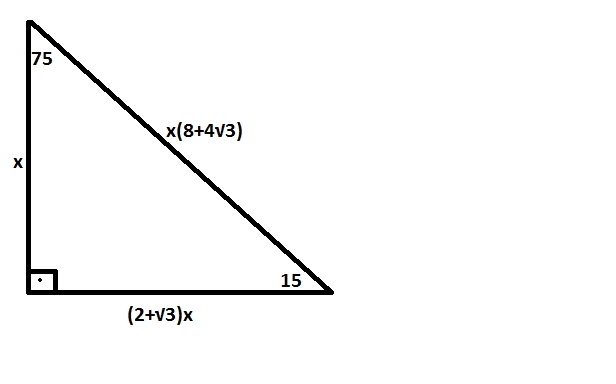



15 75 90 Ucgeni Uludag Sozluk




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube
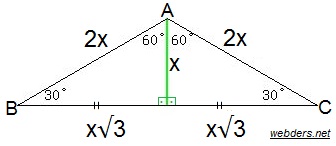



1 30 30 Ucgeni Webders Net
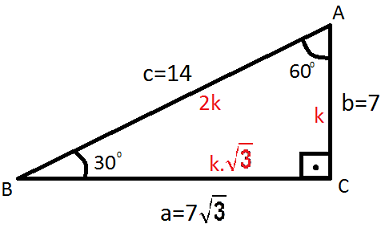



Ozel Ucgenler Cozumlu Sorular Bymutlu Com




30 60 90 Ucgeni Ve Ozellikleri Not Bu



30 60 90 Ucgeni Pisagormatik



最新 75 15 90 Ucgeni シモネタ




45 45 90 Ucgeni Ve Ozellikleri Not Bu




印刷可能 75 15 Ucgeni シモネタ



Ozel Dik Ucgenler Sanatsal Egitim



Dik Ucgende Trigonometrik Oranlar Sanatsal Egitim




Dik Ucgende Ozel Bagintilar Ppt Indir




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
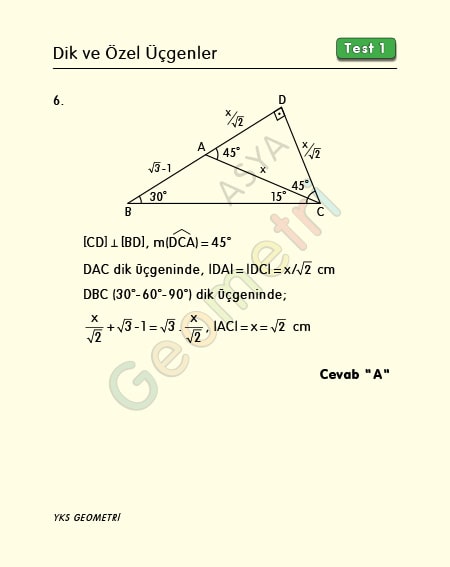



Dik Ve Ozel Ucgenler Test 1



45 45 90 Ucgeni Matematikce




Ucgenler Dik Ucgenler 4 30 60 90 Ucgeni Geometri Metin Hocam Youtube
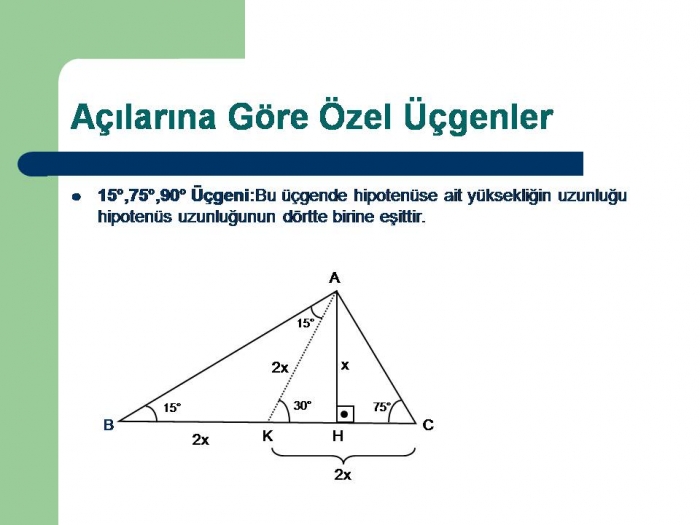



15 75 90 Ucgeni Uludag Sozluk




Eskenar Ucgenin Alan Formulunun Ispati Ve 30 60 90 Ucgeni Ozeldersci




30 60 90 Ucgeni




45 45 90 Special Right Triangle Calculator Inch Calculator




En Hizli 30 60 90 Ucgeni Ozellikleri




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




30 60 90 Ucgeni Kurali Nedir 30 60 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri




Dik Ucgen Vikipedi
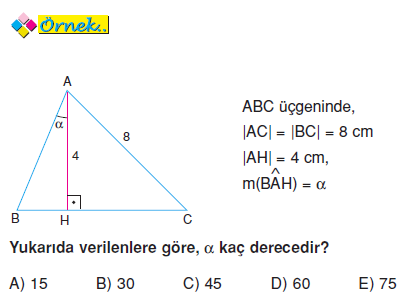



Dik Ucgen Konu Anlatimi Bilgicik Com Bilgicik Com




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger Hepsi Konu Anlatimi
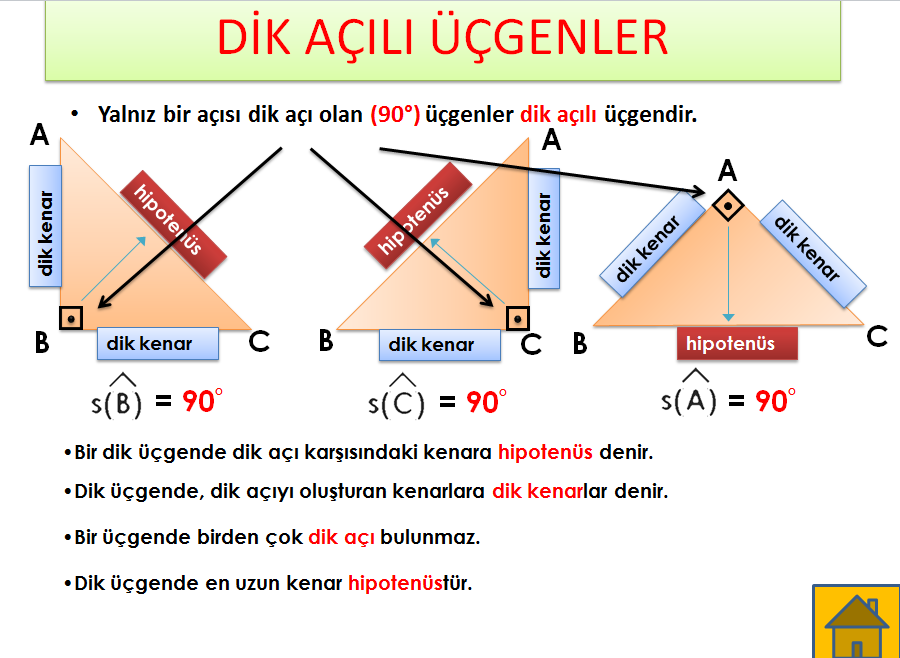



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




30 60 90 Ucgeni Akilli Geometri




Arkadaslar Yardimci Olur Musunuz 45 60 75 75 In Ordan Dik Indirdim Yine 45 30 A Ayirdim Ama Bulamadim Eodev Com
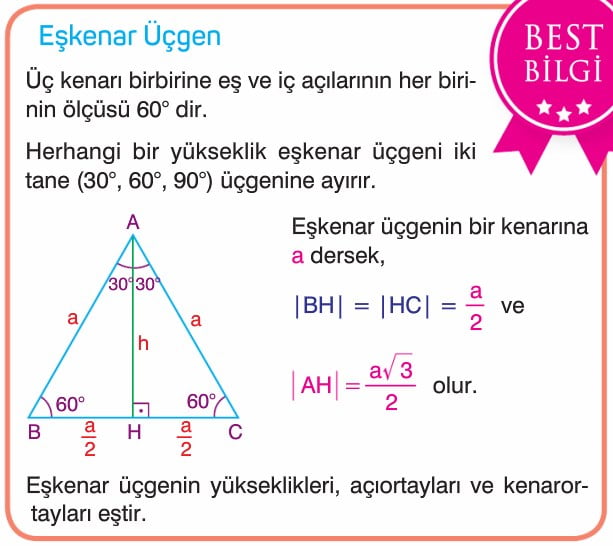



Eskenar Ucgen Konu Anlatimi Ders Notu 9 Sinif Matematik Tyt




30 60 90 Ucgeni Turleri Ve Ozellikleri
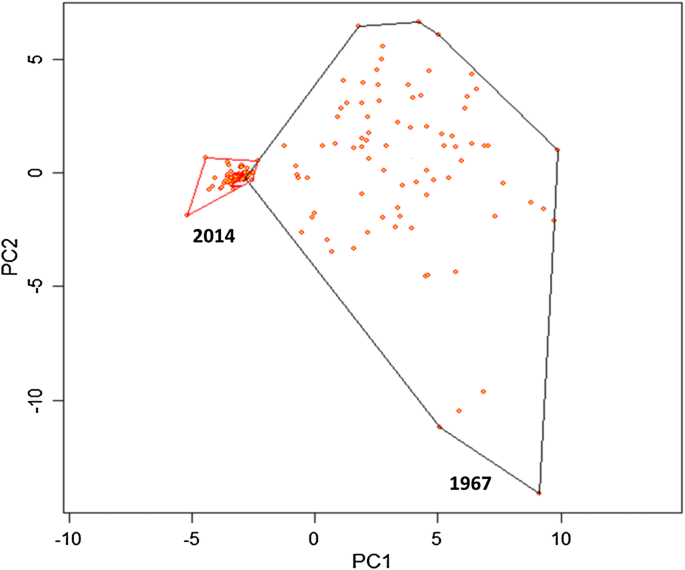



Decrease In Biodiversity In Wheat Fields Due To Changing Agricultural Practices In Five Decades Springerlink



Dik Ve Ozel Ucgenler 1




A Milk Yields And B Milk Lactose And Protein Yield During Download Scientific Diagram




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular
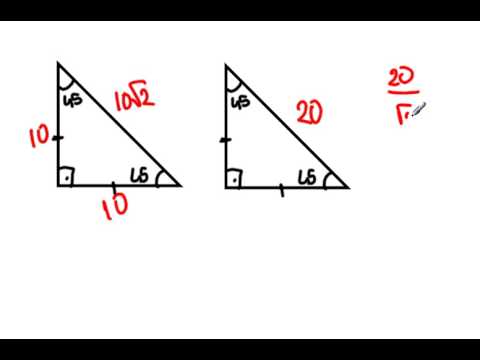



45 45 90 Ucgeni Youtube




En Hizli 30 60 90 Ucgeni Kenar
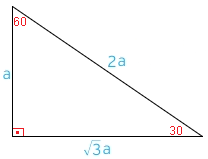



30 60 90 Ucgeni Webders Net
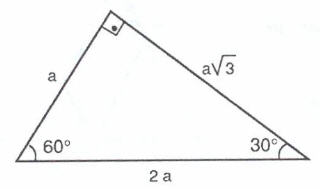



Dik Ucgen Ozellikleri




En Hizli 30 60 90 Ucgeninin Kurali




En Hizli Geometri 30 60 90 Ucgeni Ozellikleri




Eskenar Ucgen Ozellikleri Forum Tartismaforum Tartisma
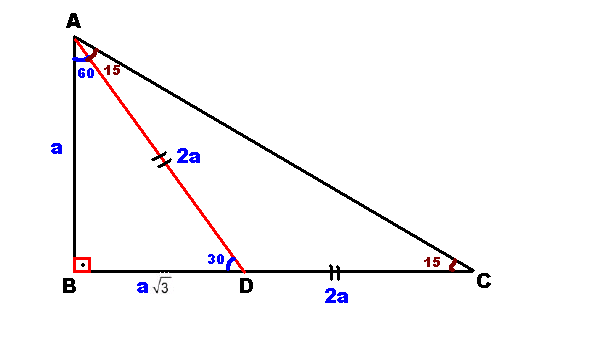



15 75 90 Ucgeni 2 3 Ispat




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List
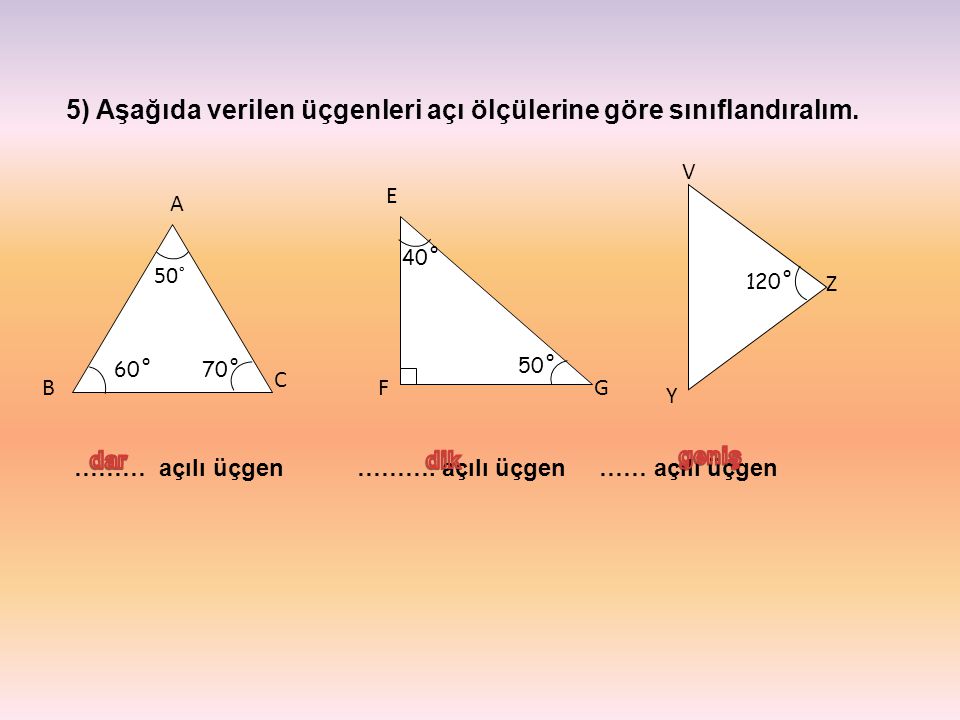



Ucgenleri Aci Olculerine Gore Siniflandirir Ppt Indir




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com
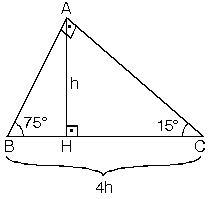



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Zoqr8sxmfxasqm




Mr Pen Architectural Ucgen Cetvel Seti 30 5 Cm Ucgen Olcek 11 Inc 30 60 Ve 8 Inc 45 90 Ucgen Amazon Com Tr Ofis Ve Kirtasiye
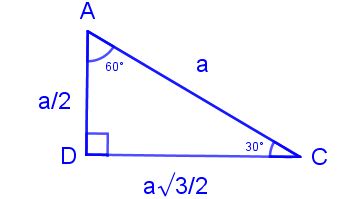



30 60 90 Ucgeni Pow Bylge



2



0 件のコメント:
コメントを投稿